M5Stack Core2でゲーム開発入門 その3 ひっくり返しロジック

2020.11.27

概要

M5Stack Core2でゲーム開発入門 その2 データ構造
概要 前回は導入まで終わらせました。今回は基本的な画像描画とデータ構造を説明したいと思います。 画像描画 #include "M5Lite.h" static LGFX_Sprite spriteBan(&M5Lite.Lcd); // R...
lang-ship.com
2020.11.20

前回は基本的な描画と、データ構造をやりました。今回は石をひっくり返すという基本的なロジックについて考えてみたいと思います。

言語化

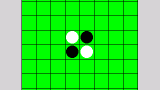
上記の①の場所に黒石を置いた場合のロジックを確認してみます。石を置くためのルールとして、一つ以上の石をひっくり返すことができるというものがあります。ひっくり返すことができる石が何石かをカウントするロジックが必要になります。

まずは８方向に対して、相手の石を自分の石ではさんでいるのかを確認する必要があります。青矢印の８方向ですね。方向別に見た場合、一石以上相手の石が置いてあり、その奥が自分の石である必要があります。このロジックを８方向に対して実装すれば良さそうですね。

実装してみる

uint8_t ban[8][8] = {
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 1, 0, 1, 0},
  {0, 0, 0, 1, 2, 2, 0, 0},
  {0, 0, 0, 2, 1, 0, 1, 0},
  {0, 0, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 0},
};

// 石が置けるかチェックする(戻り値がひっくり返す数)
int8_t isOku(int utuX, int utuY, int ishi) {
  int8_t returnIshi = 0;  // ひっくり返す石の数
  int8_t aiteIshi;        // 相手の石の色
  int8_t returnCount;     // その方向でひっくり返す石の数
  int8_t x;               // 検索対象のX座標
  int8_t y;               // 検索対象のY座標

  // 相手の石番号
  if (ishi == 1) {
    aiteIshi = 2;
  } else {
    aiteIshi = 1;
  }

  // 上方向探索
  returnCount = 0;
  for (x = utuX, y = utuY - 1; 0 <= y; y--) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 右上方向探索
  returnCount = 0;
  for (x = utuX + 1, y = utuY - 1; 0 <= y; x++, y--) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 右方向探索
  returnCount = 0;
  for (x = utuX + 1, y = utuY; x < 8; x++) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 右下方向探索
  returnCount = 0;
  for (x = utuX + 1, y = utuY + 1; x < 8; x++, y++) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 下方向探索
  returnCount = 0;
  for (x = utuX, y = utuY + 1; y < 8; y++) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 左下方向探索
  returnCount = 0;
  for (x = utuX - 1, y = utuY + 1; y < 8; x--, y++) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 左方向探索
  returnCount = 0;
  for (x = utuX - 1, y = utuY; 0 <= x; x--) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  // 左上方向探索
  returnCount = 0;
  for (x = utuX - 1, y = utuY - 1; 0 <= y; x--, y--) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      returnIshi += returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }

  return returnIshi;
}

void setup() {
  Serial.begin(115200);
  delay(1000);

  // 置ける場所を表示
  Serial.println("============================");
  for (int y = 0; y < 8; y++) {
    for (int x = 0; x < 8; x++) {
      if (ban[y][x] == 0) {
        Serial.printf("%d ", isOku(x, y, 2));
      } else if (ban[y][x] == 1) {
        Serial.print("W ");
      } else {
        Serial.print("B ");
      }
    }
    Serial.println();
  }

}

void loop() {
}

確認のために初期配置の石を変更していますが、isOku()関数を実装してみました。８方向に検索してひっくり返せる石の数をカウントして表示しています。

0 0 0 0 0 0 0 0 
0 0 0 1 1 0 0 1 
0 0 0 1 W 0 W 0 
0 0 1 W B B 0 0 
0 0 0 B W 1 W 0 
0 0 0 1 W 0 0 1 
0 0 0 0 2 1 0 0 
0 0 0 0 0 0 0 0

実行結果です。おそらくあっているとはず。。。ロジックが長くなるので、ちょっと画像表示部分をカットして、テキスト出力にしています。

最適化

さて、先程のロジックはどうでしょうか。いわゆるベタ書きのロジックです。単純な内容であればベタ書きで問題ないと思います。まずはどんなものでも動くものが書けないと意味がありません。

とはいえ、プログラムは長くなるほどバグが入りやすくなるので、可能であれば最適化をして短くしたほうが好ましいです。スッキリしたプログラムの方が処理が早い場合が多いですし、バグも減ります。

この辺は訓練なので、文章を書く場合と一緒でまずは書いてみて、その後推敲して最適化ってパターンが王道だと思います。なれてきたら推敲しながら文章を書くことができるようになります。過去に似たような物を書いたことがあると、その経験を生かしてサクッと最初から短くて推敲済みのものを書けるようになったりします。

さて、どの部分が冗長かを確認します。やはり８方向に検索している部分が同じような処理が並んでいるのでまとめたくなりますよね。

方向別判定を共通化

uint8_t ban[8][8] = {
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 1, 0, 1, 0},
  {0, 0, 0, 1, 2, 2, 0, 0},
  {0, 0, 0, 2, 1, 0, 1, 0},
  {0, 0, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 0},
};

int8_t isOkuLine(int utuX, int utuY, int ishi, int deltaX, int deltaY) {
  int8_t aiteIshi;        // 相手の石の色
  int8_t returnCount = 0; // その方向でひっくり返す石の数
  int8_t x;               // 検索対象のX座標
  int8_t y;               // 検索対象のY座標

  // 相手の石番号
  if (ishi == 1) {
    aiteIshi = 2;
  } else {
    aiteIshi = 1;
  }

  // deltaXY方向に検索
  for (x = utuX + deltaX, y = utuY + deltaY; 0 <= x && x < 8 && 0 <= y && y < 8; x += deltaX, y += deltaY) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      return returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }
  // 石をひっくり返せなかった
  return 0;
}

// 石が置けるかチェックする(戻り値がひっくり返す数)
int8_t isOku(int utuX, int utuY, int ishi) {
  int8_t returnIshi = 0;  // ひっくり返す石の数

  // 上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi,  0, -1);

  // 右上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1, -1);

  // 右方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1,  0);

  // 右下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1, +1);

  // 下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi,  0, +1);

  // 左下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1, +1);

  // 左方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1,  0);

  // 左上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1, -1);

  return returnIshi;
}

void setup() {
  Serial.begin(115200);
  delay(1000);

  // 置ける場所を表示
  Serial.println("============================");
  for (int y = 0; y < 8; y++) {
    for (int x = 0; x < 8; x++) {
      if (ban[y][x] == 0) {
        Serial.printf("%d ", isOku(x, y, 2));
      } else if (ban[y][x] == 1) {
        Serial.print("W ");
      } else {
        Serial.print("B ");
      }
    }
    Serial.println();
  }

}

void loop() {
}

isOkuLine()関数を利用して、方向を移動量のベクトルとして渡すことで共通化してみました。すこしスッキリしましたね。

さらに最適化

だいぶスッキリしましたが、まだ無駄があるロジックのようです。

  for (x = utuX + deltaX, y = utuY + deltaY; 0 <= x && x < 8 && 0 <= y && y < 8; x += deltaX, y += deltaY) {

このfor文の判定がちょっと冗長ですよね。。。XとY座標が盤面の範囲にあるかを判定しています。ここの判定がなくせるか考えてみます。

結論からいうとデータ構造を見直すことで、判定ロジックの省略が可能になります。

現状はオーソドックスなデータ配置です。8×8の配列にデータを保存しています。盤面の外にアクセスをすると関係無いデータを読み込んでしまうので、範囲外かを確認するロジックが必要でした。

そこで、盤面のデータを10×10にして、周りに壁を作ってしまいます。これにより盤面の外を参照しても大丈夫なようになります。

盤面データ構造見直し

uint8_t ban[10][10] = {
  {9, 9, 9, 9, 9, 9, 9, 9, 9, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 1, 0, 1, 0, 9},
  {9, 0, 0, 0, 1, 2, 2, 0, 0, 9},
  {9, 0, 0, 0, 2, 1, 0, 1, 0, 9},
  {9, 0, 0, 0, 0, 1, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 9, 9, 9, 9, 9, 9, 9, 9, 9},
};

int8_t isOkuLine(int utuX, int utuY, int ishi, int deltaX, int deltaY) {
  int8_t aiteIshi;        // 相手の石の色
  int8_t returnCount = 0; // その方向でひっくり返す石の数
  int8_t x;               // 検索対象のX座標
  int8_t y;               // 検索対象のY座標

  // 相手の石番号
  if (ishi == 1) {
    aiteIshi = 2;
  } else {
    aiteIshi = 1;
  }

  // deltaXY方向に検索
  for (x = utuX + deltaX, y = utuY + deltaY; ; x += deltaX, y += deltaY) {
    if (ban[y][x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y][x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      return returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }
  // 石をひっくり返せなかった
  return 0;
}

// 石が置けるかチェックする(戻り値がひっくり返す数)
int8_t isOku(int utuX, int utuY, int ishi) {
  int8_t returnIshi = 0;  // ひっくり返す石の数

  // 上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi,  0, -1);

  // 右上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1, -1);

  // 右方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1,  0);

  // 右下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1, +1);

  // 下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi,  0, +1);

  // 左下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1, +1);

  // 左方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1,  0);

  // 左上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1, -1);

  return returnIshi;
}

void setup() {
  Serial.begin(115200);
  delay(1000);

  // 置ける場所を表示
  Serial.println("============================");
  for (int y = 1; y <= 8; y++) {
    for (int x = 1; x <= 8; x++) {
      if (ban[y][x] == 0) {
        Serial.printf("%d ", isOku(x, y, 2));
      } else if (ban[y][x] == 1) {
        Serial.print("W ");
      } else {
        Serial.print("B ");
      }
    }
    Serial.println();
  }
}

void loop() {
}

データ構造に手をいれたことで、判定ロジックが減りました。繰り返し系の中にある判定は減らすと全体的な速度がかなり向上します。

さらに最適化できるか考える

uint8_t ban[10][10] = {
  {9, 9, 9, 9, 9, 9, 9, 9, 9, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 1, 0, 1, 0, 9},
  {9, 0, 0, 0, 1, 2, 2, 0, 0, 9},
  {9, 0, 0, 0, 2, 1, 0, 1, 0, 9},
  {9, 0, 0, 0, 0, 1, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 0, 0, 0, 0, 0, 0, 0, 0, 9},
  {9, 9, 9, 9, 9, 9, 9, 9, 9, 9},
};

データを二次配列で保存していますが、一次配列の方がアクセスが早い場合があります。

uint8_t ban[10 * 10] = {
  9, 9, 9, 9, 9, 9, 9, 9, 9, 9,
  9, 0, 0, 0, 0, 0, 0, 0, 0, 9,
  9, 0, 0, 0, 0, 0, 0, 0, 0, 9,
  9, 0, 0, 0, 0, 1, 0, 1, 0, 9,
  9, 0, 0, 0, 1, 2, 2, 0, 0, 9,
  9, 0, 0, 0, 2, 1, 0, 1, 0, 9,
  9, 0, 0, 0, 0, 1, 0, 0, 0, 9,
  9, 0, 0, 0, 0, 0, 0, 0, 0, 9,
  9, 0, 0, 0, 0, 0, 0, 0, 0, 9,
  9, 9, 9, 9, 9, 9, 9, 9, 9, 9,
};

こんな感じの一次配列に変換します。

    if (ban[y * 10 + x] == aiteIshi) {
      // 相手の石
      returnCount++;
    }

アクセスする場合には上記のように「y * 10 + x」でインデックスを計算します。今回は実行時間を計測していませんが、本来は実行時間やビルド時のサイズを確認しながら最適化をする必要があります。

もっと最適化できるか？

一次配列化をしたことにより、実は上記の色がついているデータが必要ありません。

インデックスで考えるとわかりやすいのですが、本来一次配列なので横に並んでいます。

それを擬似的に横10個で区切ってアクセスしています。

色がついていた場所を削ると上記の形になります。一次配列なので、実は削った場所にもアクセスすることができます。

削られた場所は、次のインデックスにアクセスするので上記のような形でアクセスが可能です。

最終的なスケッチ

uint8_t ban[91] = {
  9, 9, 9, 9, 9, 9, 9, 9, 9,
  9, 0, 0, 0, 0, 0, 0, 0, 0,
  9, 0, 0, 0, 0, 0, 0, 0, 0,
  9, 0, 0, 0, 0, 1, 0, 1, 0,
  9, 0, 0, 0, 1, 2, 2, 0, 0,
  9, 0, 0, 0, 2, 1, 0, 1, 0,
  9, 0, 0, 0, 0, 1, 0, 0, 0,
  9, 0, 0, 0, 0, 0, 0, 0, 0,
  9, 0, 0, 0, 0, 0, 0, 0, 0,
  9, 9, 9, 9, 9, 9, 9, 9, 9, 9,
};

int8_t isOkuLine(int utuX, int utuY, int ishi, int deltaX, int deltaY) {
  int8_t aiteIshi;        // 相手の石の色
  int8_t returnCount = 0; // その方向でひっくり返す石の数
  int8_t x;               // 検索対象のX座標
  int8_t y;               // 検索対象のY座標

  // 相手の石番号
  if (ishi == 1) {
    aiteIshi = 2;
  } else {
    aiteIshi = 1;
  }

  // deltaXY方向に検索
  for (x = utuX + deltaX, y = utuY + deltaY; ; x += deltaX, y += deltaY) {
    if (ban[y * 9 + x] == aiteIshi) {
      // 相手の石
      returnCount++;
    } else if (ban[y * 9 + x] == ishi) {
      // 自分の石なので間の石がひっくり返せる石
      return returnCount;
      break;
    } else {
      // 石がない場合は終了
      break;
    }
  }
  // 石をひっくり返せなかった
  return 0;
}

// 石が置けるかチェックする(戻り値がひっくり返す数)
int8_t isOku(int utuX, int utuY, int ishi) {
  int8_t returnIshi = 0;  // ひっくり返す石の数

  // 上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi,  0, -1);

  // 右上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1, -1);

  // 右方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1,  0);

  // 右下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, +1, +1);

  // 下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi,  0, +1);

  // 左下方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1, +1);

  // 左方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1,  0);

  // 左上方向探索
  returnIshi += isOkuLine(utuX, utuY, ishi, -1, -1);

  return returnIshi;
}

void setup() {
  Serial.begin(115200);
  delay(1000);

  // 置ける場所を表示
  Serial.println("============================");
  for (int y = 1; y <= 8; y++) {
    for (int x = 1; x <= 8; x++) {
      if (ban[y * 9 + x] == 0) {
        Serial.printf("%d ", isOku(x, y, 2));
      } else if (ban[y * 9 + x] == 1) {
        Serial.print("W ");
      } else {
        Serial.print("B ");
      }
    }
    Serial.println();
  }
}

void loop() {
}

上記がとりあえず最適化完了したスケッチ例です。今回はここまでにしますが、もう少し最適化は可能です。検索する方向はX座標とY座標個別に渡していますが、データ構造を考慮すれば「deltaY * 9 + deltaX」で一次配列のインデックス差分を渡したほうが処理が減らせます。

また、今回は白と黒で共通関数ですが、実は黒番と白番で別関数にして変数との判定ではなく、直値での判定にしたほうがコンパイラの最適化で早くなったりもします。

まとめ

最適化はどこまでやるのかは非常に難しいです。個人的には遅くて困ってから最適化をすればいいと思っていますが、ソースコードの保守を考えると適度に最適化をしたほうがスッキリして読みやすいコードになります。

ガリガリに最適化をしてしまうと、逆に他の人が読んだ場合に理解しにくいものになります。このへんのバランスは状況によって変わってくるとは思います。

個人的には、まずはベタ書きでも動くことが最重要だと思います。最適化はあとですればいいので、まずは動いていないとなにも始まらないです。できれば、２段階目の同じようなロジックを共通化するところまでは実施したほうがいいと思っています。

そのさきの最適化は、、、んー。普通のゲームであれば必要ないと思います。シューティングなどであればロジックの速度が重要になるので、パズルみたいな最適化が必要になると思いますが、オセロが題材であればベタ書きロジックでも速度的な問題は起こりにくいと思います。

ただし、オセロでもコンピューターオセロなどの昔ながらのAIを作ろうとした場合には、ある程度最適化しないと厳しいと思っています。

続編

M5Stack Core2でゲーム開発入門 その4 サウンド
概要 前回はロジックとデータ構造について説明をしました。今回はサウンド周りを解説してみたいと思います。 ESP32でのサウンド まずは一般的なESP32でのサウンド処理について説明をしてみたいと思います。 PWMでの圧電スピーカー 一番原始...
lang-ship.com
2020.12.08

コメント